Vector Transformations with World Matrices
At a Glance
- World matrices map a vector from an entity’s local space (body frame) to the world space (world frame)
- Vectors in Space Engineers are considered row major when doing operations with matrices
Intro
Vector transformations are a bit difficult to understand, so I figured I’d put together a little guide to help y’all use this incredibly helpful tool in your programs :)
Transformations are an incredibly powerful tool that can help simplify 3D problems!
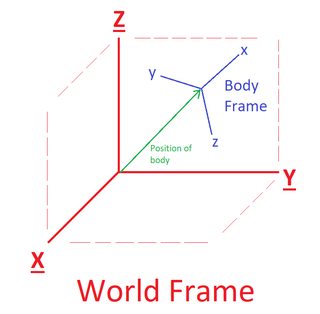
World vs. Body Coordinate Frames
The important coordinate frames that I will speak of come in 2 varieties: World and Body.
A World frame is a coordinate system that stays stationary. The origin does not move, nor do the X ,Y, or Z axes. This is often called the “ground frame” in Earth based engineering applications. The GPS in-game uses the world frame for example.
A Body frame is a coordinate system that is affixed to a particular body (or entity) within the world frame. The origin of this Body frame is free to translate in the world frame, and the local x, y, and z axes of the Body frame can rotate relative to the stationary World frame. This is also sometimes called a “local” frame since it is local to a particular body.
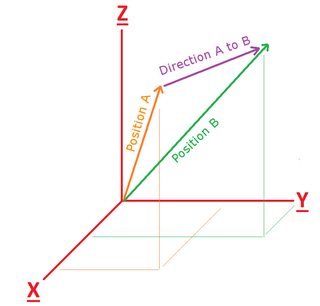
Direction Vectors vs. Position Vectors
Now let’s clarify the difference between position vectors and direction vectors.
A direction vector simply defines a magnitude and a direction. Examples of direction vectors are velocity and acceleration. They define magnitudes (speed and acceleration) and the direction that that points.
A position vector is a special kind of direction vector that is used to define a point in space measured from the origin of a coordinate system. GPS position is a good example of this.
In other words: all position vectors are direction vectors, but not all direction vectors are position vectors.
Often times we want the position of an object relative to another object.
In this example, Position A and Position B are position vectors in the world frame. Direction A to B is a direction vector in the world frame that specifies the direction towards B from A.
To get this direction vector we simply subtract! <Direction vector> = <End position vector> - <Start position vector>
Thus: <Direction A to B> = <Position B> - <Position A>
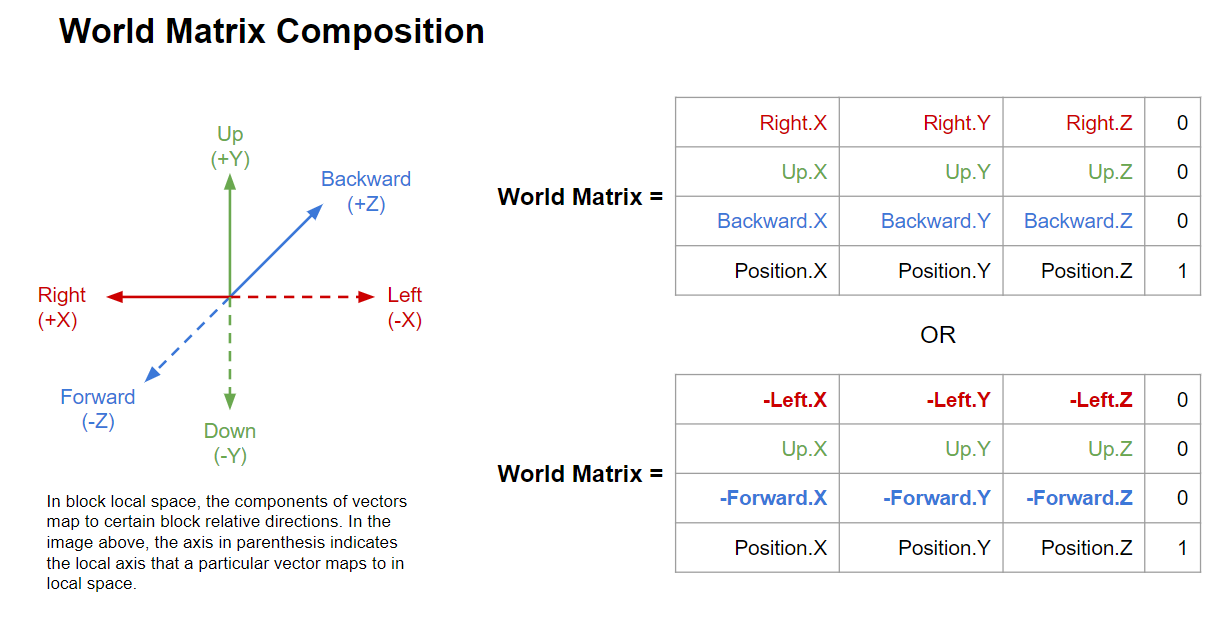
Composition of a World Matrix
A Space Engineers world matrix maps a vector from a entity’s body space to world space. (Blocks and CubeGrids have world matrices as well as most other objects in the game!)
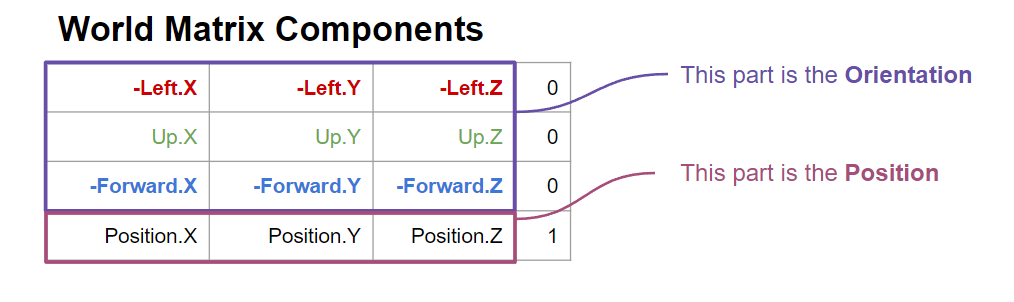
The first 3 rows of the World Matrix specify the orientation of the body’s direction vectors in world space. The 4th row specifies the location of the body frame within the world frame. (The 0’s and the 1 in the last column are simply placeholders since Vrage’s matrices are 4x4)
We can use this information to easily convert between body and world frames!
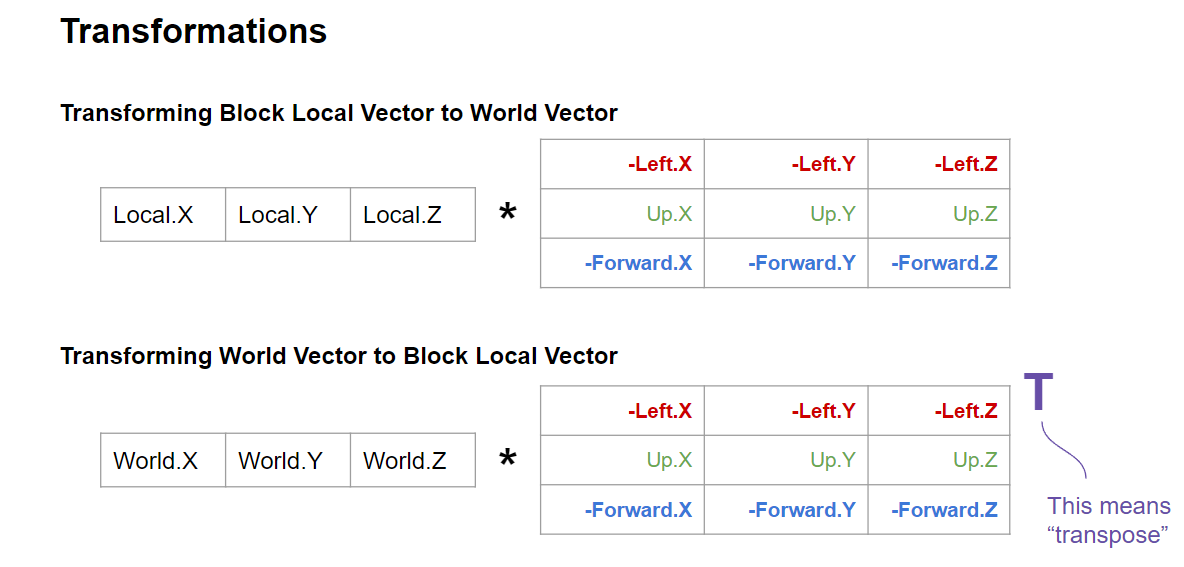
Also, in local space, the components of the vector mean specific things. In Space Engineers: +X is Right, +Y is Up, and +Z is Backwards in local space. I prefer Left-Up-Forward notation, but the math is the same as Right-Backwards-Up with some sign changes (as seen in the figures above). Since the world matrix is given to you by the game in most instances, you need not worry about this too much; it is merely two ways to represent the same information. The math is mostly abstracted away from you within the Vector3D.Transform and Vector3D.TransformNormal methods to be introduced soon…
Transformations!!!
Now, you may be asking “What the heck is a Transformation”? Sounds pretty scary and complex, right? Nope!
In Space Engineers, a transformation is simply a matrix-vector multiplication!
Vector transformations allow you to do cool things like convert a world velocity to a block relative local velocity!
(Note that the math above is for direction vectors)
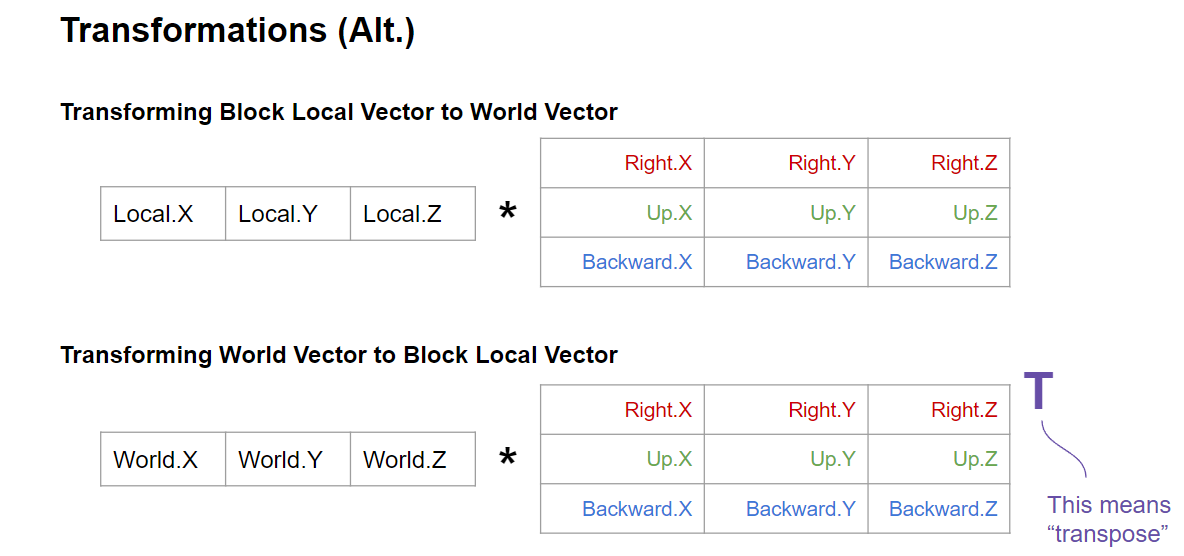
Right-Backwards-Up Notation
The math is exactly the same, we just use the opposite directions to get rid of negative signs.
In General:
- Use Vector3D.TransformNormal() for direction vectors (velocity, acceleration, relative positions)
- Use Vector3D.Transform() for position vectors (but not world to body position transforms)
Body Direction to World Direction
For direction vectors we use Vector3D.TransformNormal() and the world matrix.
Vector3D bodyDirection = new Vector3D(1,2,3);
IMyTerminalBlock referenceBlock = SomeFunctionToAssignThisBlock();
// Convert the local vector to a world direction vector
Vector3D worldDirection = Vector3D.TransformNormal(bodyDirection, referenceBlock.WorldMatrix);
World Direction to Body Direction
To go from world direction to body directions, we use Vector3D.TransformNormal() and the transposed world matrix.
Vector3D worldDirection = new Vector3D(69,69,69); //giggle
IMyTerminalBlock referenceBlock = SomeFunctionToAssignThisBlock();
// Convert worldDirection into a local direction
Vector3D bodyVector = Vector3D.TransformNormal(worldDirection, MatrixD.Transpose(referenceBlock.WorldMatrix)); // Note that we transpose to go from world -> body
Body Position to World Position
To transform a body position to a world position, we use Vector3D.Transform() and the world matrix.
Vector3D bodyPosition = new Vector3D(1,2,3);
IMyTerminalBlock referenceBlock = SomeFunctionToAssignThisBlock();
Vector3D worldPosition = Vector3D.Transform(bodyPosition, referenceBlock.WorldMatrix); // Note no longer TransformNormal
Note how we used Transform instead of TransformNormal because this was a position vector.
Alternative Method
Vector3D bodyPosition = new Vector3D(1,2,3);
IMyTerminalBlock referenceBlock = SomeFunctionToAssignThisBlock();
// Get world position of the local origin
Vector3D referenceWorldPosition = referenceBlock.WorldMatrix.Translation;
// Convert the local vector to a world direction vector
Vector3D worldDirection = Vector3D.TransformNormal(bodyPosition, referenceBlock.WorldMatrix);
// Combine origin position and world direction
Vector3D worldPosition = referenceWorldPosition + worldDirection;
World Position to Body Position
This is a special case!
In order to avoid performance heavy math, we change the world position vector into a world direction vector before our transform. This allows us to avoid using a matrix inversion (avoid these for better performance in your codes).
In this method we use Vector3D.TransformNormal() and a transposed world matrix.
Vector3D worldPosition = new Vector3D(69,69,69); // Giggle...
IMyTerminalBlock referenceBlock = SomeFunctionToAssignThisBlock();
Vector3D referenceWorldPosition = referenceBlock.WorldMatrix.Translation; // block.WorldMatrix.Translation is the same as block.GetPosition() btw
// Convert worldPosition into a world direction
Vector3D worldDirection = worldPosition - referenceWorldPosition ; // This is a vector starting at the reference block pointing at your desired position
// Convert worldDirection into a local direction
Vector3D bodyPosition = Vector3D.TransformNormal(worldDirection, MatrixD.Transpose(referenceBlock.WorldMatrix)); // Note that we transpose to go from world -> body
Alternative Method (NOT RECOMMENDED)
In this method we use Vector3D.Transform() and an INVERTED world matrix.
Vector3D worldPosition = new Vector3D(69,69,69); // Giggle...
IMyTerminalBlock referenceBlock = SomeFunctionToAssignThisBlock();
Vector3D bodyPosition= Vector3D.Transform(localVector, MatrixD.Invert(referenceBlock.WorldMatrix)); // Note no longer TransformNormal
// Also, matrix inversions are bad!
This is notably less performant than the above method since it needs a full matrix inversion as opposed to a simple matrix transpose.
A big thank you goes to Whiplash141 for writing this tutorial. This tutorial was adapted from the original on Malware's MDK wiki, by Malware.